Binarne rączki - postscriptum dla dorosłych

Dawno, dawno temu, w pewien piękny lipcowy poranek wrzuciłam do szuflady świadectwo ukończenia pierwszej klasy liceum (odpowiednik obecnej trzeciej klasy gimnazjum), spakowałam plecak i wyruszyłam do Milicza na wakacyjny obóz przysposobienia obronnego, gdzie przez miesiąc miałam bawić się w wojsko w towarzystwie rówieśnic z całego Dolnego Śląska. Zabawa była przednia, pomimo wyjątkowego w tamtym roku urodzaju na komary, które przeprowadziły zmasowany desant na milickie stawy. Był to pierwszy w moim nastoletnim życiu szerszy kontakt z uczniami innych szkół średnich niż licea. Dyskretnie obserwowałam dziewczyny z technikum, niczym przedstawicielki jakieś rzadkiego, egzotycznego gatunku. Fascynacja była obopólna, aż wreszcie ciekawość zwyciężyła i koleżanki z "mechanicznego" postanowiły wysondować wiedzę matematyczną tych z ogólniaka. 

- Ty chodzisz do mat-fizu, prawda?

- No.

- A umiesz zamienić liczbę na inny układ?

- ????

- No, na przykład na dwójkowy, albo na piątkowy, wszystko jedno.

- Yyyy..., oczywiście że umiem, a ty umiesz? Uczą was takich rzeczy w technikum? - odbiłam piłeczkę, starając się zyskać na czasie. Ostatecznie ustaliłyśmy, że każda z nas zrobi obliczenia na swojej kartce, a potem porównamy wyniki.

Zadanie miało polegać na zamianie zapisu dziesiętnego na dwójkowy. Nie pamiętam już, jaką liczbę wzięłyśmy na warsztat, ale nie ma to większego znaczenia. Przyjmijmy, że była to liczba 586, bohaterka pierwszego odcinka "Binarnych rączek". Dziewczyny zabrały się do pracy. Widać było, że piszą coś z dużą wprawą, nie zatrzymując się nad kolejnymi krokami. Ja nie dysponowałam żadnym wypróbowanym algorytmem, którym mogłabym się posłużyć. Niczym, poza teoretyczną wiedzą, że zapis dwójkowy skonstruowany jest na podobnej zasadzie, jak zapis dziesiętny. Nakazałam sobie spokój. Zaraz, zaraz... Najpierw trzeba znaleźć największą potęgę dwójki, która "zmieści się" w mojej liczbie. Zaczęłam szybko wyliczać kolejne potęgi: 2, 4, 8, 16, 32, 64, 128, 256, 512... dobra mam ją! 512 to dziewiąta potęga dwójki, więc mój zapis będzie miał 10 cyfr. Na pierwszym miejscu, wiadomo - jedynka, innej opcji nie ma: 1_ _ _ _ _ _ _ _ _, Jeszcze tylko 9 cyfr i gotowe :-). Po odjęciu 512 od wyjściowej liczby pozostaje mi do rozdysponowania liczba 74. 256 się w niej nie zmieści, 128 też nie, więc w zapisie przybywają dwa zera: 100_ _ _ _ _ _ _. Największa pasująca potęga dwójki to 64. Kolejna jedynka w zapisie: 1001 _ _ _ _ _ _ i z wyjściowej liczby pozostało już tylko 10. Liczba 32 jest od 10 większa, 16 również, więc zapis wzbogaca się o dwa kolejne zera: 100100 _ _ _ _. A następnie o jedynkę, kiedy od pozostałej dziesiątki odejmę 8: 1001001 _ _ _ . Dobra nasza, pozostała mi już tylko dwójka. Liczba 4 jest od niej większa, więc dopisuję kolejne zero: 10010010 _ _ ... i na kolejnym miejscu, po "skasowaniu" tej ostatniej dwójki, jedynkę: 100100101 _. Na placu boju zostaje zero, które ląduje na ostatnim miejscu zapisu: 1001001010. Mam nadzieję, że się nigdzie nie pomyliłam. Dziewczyny są już gotowe, więc na sprawdzanie nie ma czasu. Pokazuję swój zapis, one swój:

????

- Zaraz, to co wam w końcu wyszło?

- No, te zera i jedynki po prawej stronie kreski, trzeba na nie patrzeć od końca. Strasznie długo liczyłaś, ale wyszło ci tak samo.

- Faktycznie... Ale jak to policzyłyście?

- Normalnie, dzieli się liczbę przez dwa, wynik się pisze pod spodem, a resztę z dzielenia po prawej. I tak dalej, aż na dole zostanie zero.

- Aha... A dlaczego tak? Skąd wiadomo, że to jest dobrze?

- Pani nam tak podała, to musi być dobrze. Zresztą wyszło nam tak samo jak tobie.

Rzeczywiście wyszło tak samo i raczej nie był to przypadek, ale nie rozumiałam, dlaczego tak się stało i na czym polega sposób koleżanek z technikum. Próbowałam wytłumaczyć im swoją metodę, ale niespecjalnie mi to wychodziło.

- Wolimy nasz sposób, jest szybszy i nie trzeba kombinować - skwitowały moje usiłowania.

Próbowałam się pocieszać, że ja przynajmniej rozumiem co robię, ale słaba to była pociecha. Po pierwsze, moje zrozumienie też nie było dogłębne. Posłużyłam się raczej analogią do zapisu dziesiętnego, nie zgłębiając jego istoty. A po drugie, gdzieś z tyłu głowy kołatało mi się męczące przekonanie, że mój sposób ma niewiele wspólnego z liczeniem. A przecież zapis dziesiętny wymyślono, żeby łatwiej można było policzyć to, na co nie wystarcza dziesięciu palców. Sposób koleżanek wydawał mi się pod tym względem bardziej obiecujący. Gdyby tylko udało mi się go rozgryźć... Ale poobiedni odpoczynek dobiegał końca i kompania szykowała się już do wymarszu na strzelnicę. Niczym Scarlett O'Hara, odłożyłam myślenie do następnego dnia.

Ale następnego dnia było ognisko, potem wyprawa nad jezioro i ani się obejrzałam, kiedy wakacje minęły i sprawa zapisu pozycyjnego została odłożona ad acta. W szkole były pilniejsze sprawy, a w razie potrzeby przecież umiałam sobie poradzić...

Olśnienie przyszło nagle, po wielu latach, nad stertą rozsypanych przez niecierpliwe rączki klocków, które próbowaliśmy wspólnie policzyć.

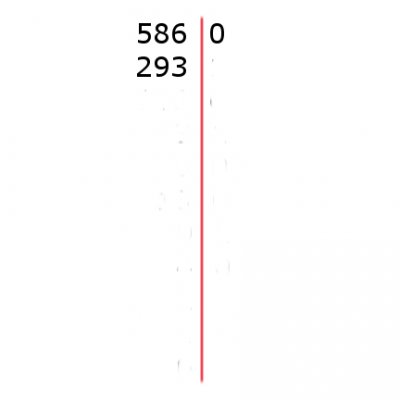
Tak, to było to! Grupowanie klocków po dwa, to przecież nic innego, jak dzielenie ich liczby przez dwa.

Oczywiście z resztą, która w tym wypadku wyniosła zero, bo żaden pojedynczy klocek nam nie został:

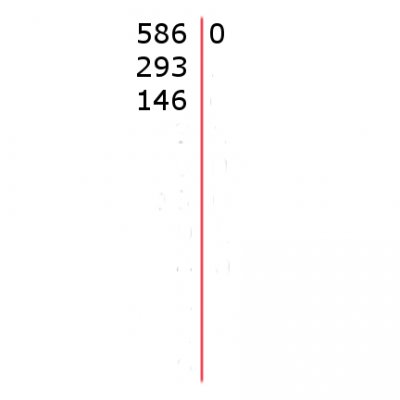
Dwójki znów grupowaliśmy po dwie, czyli dzieliliśmy ich liczbę przez dwa:

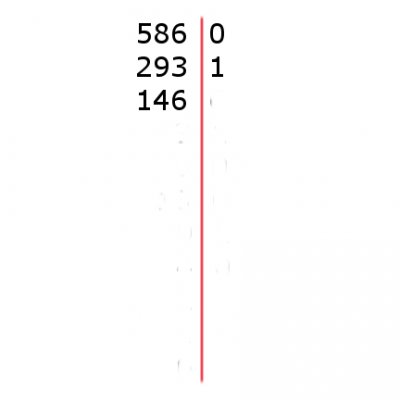
Tym razem jedna dwójka została bez pary, więc reszta z dzielenia wyniosła jeden:

I tak dalej, aż wszystkie klocki zostały zagospodarowane. Przeczucie mnie nie zawiodło: sposób koleżanek doskonale się nadawał do przeliczania dużych zbiorów. Ma on przy tym tę zaletę, że może w nim uczestniczyć wiele osób i praktycznie wyeliminowane jest ryzyko popełnienia błędu.

Możnaby na przykład w krótkim czasie przeliczyć w ten sposób uczestników masowej imprezy plenerowej, uzyskując dokładny wynik i mając przy tym mnóstwo zabawy. W odróżnieniu od wielu innych zabaw z matematyką w tle, tutaj bawiliby się wszyscy obecni, łącząc pożyteczne z przyjemnym.

1. W pierwszym kroku każdy stara się znaleźć sobie parę. Ktoś oczywiście musi wziąć na siebie rolę wodzireja, wydając stosowne komendy przez megafon. Potrzebni też będą ochotnicy, wyposażeni w duże plansze z zerem po jednej stronie i jedynką po drugiej.

Na dwoje babka wróżyła: albo wszystkim uda się połączyć w pary, co będzie oznaczało, że liczba uczestników zabawy jest parzysta, albo pozostanie jeden "singiel". W naszej wirtualnej symulacji zachodzi ten pierwszy przypadek. Na scenie pojawia się osoba trzymająca planszę z zerem.

2. W kolejnym kroku pary szukają sobie par. Tym razem jedna para pozostaje na środku placu...

... a na scenie obok zera pojawia się jedynka.

3. Czwórki znów łączą się w pary, tworząc ósemki.

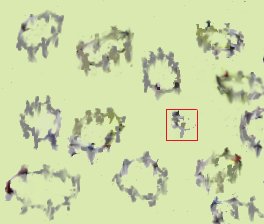
Żadna czwórka nie pozostała bez pary więc przed jedynką pojawia się zero.

4, Ósemki łączą się, tworząc szesnastki. Znów bez reszty.

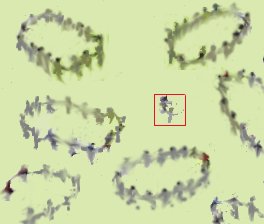
W zapisie przybywa kolejne zero.

5. Przy łączeniu szesnastek jedna z nich pozostała bez pary. Na środku placu znajduje się więc teraz jedna dwójka i jedna szesnastka...

... a na scenie pojawia się jedynka.

6. W trzech kolejnych próbach łączenie coraz większych grup w pary udaje się przeprowadzić bez reszty. W zapisie przybywają trzy kolejne zera.

7. W następnym kroku pozostaje reszta. Grupa "bez pary", znacznie większa niż poprzednie, otacza kręgiem szesnastkę i dwójkę...

... a w zapisie przybywa jedynka.

Zabawa jest kontynuowana, dopóki każdy z uczestników nie znajdzie się w jednym z koncentrycznych kręgów, reprezentujących kolejne "reszty". Tak wygląda ostateczny zapis dwójkowy liczby wszystkich uczestników:

Kto podpowie, ile osób brało udział w zabawie?